CSCI 200 - Foundational Programming Concepts & Design - Fall 2022

This lab is due by Tuesday, December 06, 2022, 11:59 PM.
As with all labs you may, and are encouraged, to pair program a solution to this lab. If you choose to pair program a solution, be sure that you individually understand how to generate the correct solution.

Instructions

Your task for this assignment is to read in a star data file, store the data in a list of objects, make modifications to the data, and then draw a star map similar to the one shown here:

We'll begin by describing the data to store. Then the following sections will describe how to store and modify the data. The final sections will describe how to display the data.

Data File

To begin, use the appropriate SFML project template and place the stars.txt file in the data directory.

Each line of the data file contains information of one star, with each field separated by a tab. The meaning of each field (column) is described below. Note that data files often contain more information than is needed for a given purpose and that data files may contain outlying values that are also not needed for a given purpose. We suggest you take a look at the stars.txt file as you read the following details about your input file.

• The first three fields are the x, y, and z coordinates for the star. You will need to store the x and y coordinates, but will not need the z coordinate.
• The fourth field is the brightness of each star.
• The fifth and sixth fields are the Henry Draper and Harvard Revised numbers for the star. These are numbers used in different star catalog systems, so they can be ignored for this assignment.

Star Class

We now need to create a class to store the data that represents a single star. Create a Star class in its own header and implementation file. Our class must have the following members:

• A private data member to store the x coordinate
• A private data member to store the y coordinate
• A private data member to store the brightness value
• A default constructor that sets all data members to zero
• A parameterized constructor that sets each data member accordingly
• The corresponding public getter/setter methods

We now can read and parse the data file. While doing so, we will want to create a star object for each record. We will then store each object in a vector of stars. However, we only want to create and store stars that have a brightness within the inclusive range of 0.0 to 8.0.

At this point your program should open, read, and store the valid stars into a vector of Star objects. The given star file has 3,521 valid stars to check your progress thus far.

Modify the Coordinates

We are able to store the stars with their data represented in the original format. We will need to manipulate the data to have it in a form that will work with our program and ultimately be able to plot them visually. The first manipulation we do will relates to the (x, y) coordinate the star exists at.

Each axis in the star coordinate system goes from -1.0 to +1.0 and the origin (0, 0) is at the center. Thus, the x and y coordinate values for each star will all be numbers in the range -1.0 to +1.0.

The coordinate system used in our graphics library (SFML) has the origin (0, 0) in the upper-left corner of the picture, and the maximum x and y values are the width and height of the window, in pixels.

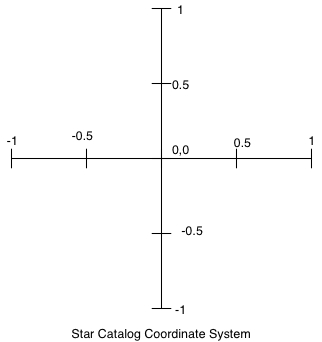
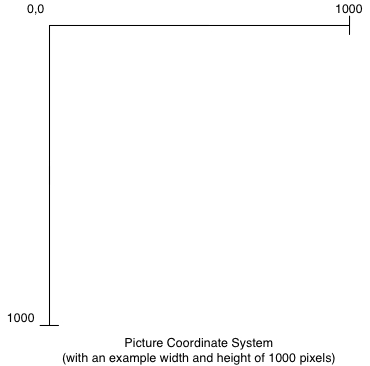
Thus, to determine the location of each star to draw in our graphics library, you need to convert from the -1.0 to +1.0 range of the star coordinate system to the (0, 0) to (WIDTH, HEIGHT) range of the graphics library coordinate system. Declare WIDTH and HEIGHT as constants in your program, with both values set to 640 (which are defined for your screen size).

More specifically, if xStar is a double variable holding a star's x-coordinate in the range -1.0 to +1.0, to convert it to an integer pixel value in the range 0 to WIDTH, you would use the following:

xPixel = ( xStar + 1 ) * WIDTH / 2;

Similarly, if yStar is a double variable holding a star's y-coordinate in the range -1.0 to +1.0, to convert it to an integer pixel value in the range 0 to HEIGHT, you would use the following:

yPixel = ( -yStar + 1 ) * HEIGHT / 2;

Note the minus sign on the yPixel equation. We encourage you to plug a few coordinates into these equations, e.g., (-0.5,0.5) and (-0.5,-0.5), to ensure the equations are correct.

Add two public functions to our Star class matching the following specifications:

• getTransformedX()
  Input: the WIDTH of the window
  Output: a float
  Task: compute the raw star x coordinate transformed in to the window coordinate
• getTransformedY()
  Input: the HEIGHT of the window
  Output: a float
  Task: compute the raw star y coordinate transformed in to the window coordinate

To verify the modifications are correct, the first line of the stars.txt file is:

0.994772	-0.023164	-0.099456	4.610000	28	3

If our window is sized 640x640, then the first star would be transformed to (638.327, 327.412).

Drawing a Star

In your code, you'll need to draw each star. Since stars look like circles, use the CircleShape class. Each circle needs a non-zero radius; use the setRadius function to set this to 2. Then, use this starShape object to draw each star with its corresponding properties (i.e., coordinates and brightness). For example, to set a star at position xPixel and yPixel use the following:

starShape.setPosition(Vector2f(xPixel, yPixel));

A star can be drawn on the window using the following function call:

window.draw(starShape);

We should now be able to successfully run our program and see a visualization of the stars, as seen below.

They are all placed in the correct position, but all equally bright. Read on about how the brightness will affect the coloring of each star.

Shades of Gray

One of the most common ways to represent colors is with the RGB color model. In this model, each color is represented with three numbers in the range 0 to 255 that represent the amount of red, green, and blue to include in the color. For example, (255,0,0) is the color red and (255,255,0) is the color yellow (i.e., red and green combined). Any color with the same amount of red, green, and blue is a shade of gray. We will use shades of gray to draw our stars with different brightness; thus, in this project, you should include the same amount of red, green, and blue in your colors drawn.

SFML has a Color class that allows the drawing of specific colors using the RGB model. For example, each of the following examples sets the fill color of a starShape to a different shade of gray:

// Black
starShape.setFillColor(Color(0, 0, 0));
// Dark gray
starShape.setFillColor(Color(64, 64, 64));
// Medium gray
starShape.setFillColor(Color(128, 128, 128));
// Light gray
starShape.setFillColor(Color(192, 192, 192));
// White
starShape.setFillColor(Color(255, 255, 255));

To determine the shade of gray for each star drawn in this project, you need to scale the brightness value of the star to an integer value between 0 and 255 and set the fill color using that value, as shown above. For example, if brightness is a double variable holding a star's brightness value in the range 0.0 to BRIGHTEST_STAR, to convert it to an integer value in the range 0 to 255, you would use the following:

int shadeOfGray = (int)( ( 255.0 * brightness ) / BRIGHTEST_STAR );

You would then use this shadeOfGray variable to set the drawing color and fill color:

starShape.setFillColor(Color(shadeOfGray, shadeOfGray, shadeOfGray));

However, we would much rather encapsulate this calculation within the Star class. Add another public function to your Star class with the following specifications:

• getGrayscaleColor()
  Input: the value of the brightest star from the list of valid Stars
  Output: a SFML Color object
  Task: create the grayscale Color based on the calculations above

Adding in the grayscale for each star will result in the following dimmed image:

This is completing the task, however we are interpreting the brightness values incorrectly. In the star system format, 0.0 represents what should be the brightest star and a larger value signifies the darker a star should appear. Therefore, when calculating the shadeOfGray value, we need to "invert" the value of the brightness before performing the grayscale calculation:

invertedBrightness = BRIGHTEST_STAR - brightness;

Now when plotting the stars, the edge is dimmer and the brightest star is at the center of the map:

Lab Submission

Submit your main.cpp, Star.h, Star.cpp, Makefile file(s).

You will submit your solution to this lab with the rest of Set6. Detailed instructions for doing this are posted in Assignment 6.

This lab is due by Tuesday, December 06, 2022, 11:59 PM.
As with all labs you may, and are encouraged, to pair program a solution to this lab. If you choose to pair program a solution, be sure that you individually understand how to generate the correct solution.